Hanc primam esse consonantiarum omnium, & quae facillime post vnisonum auditu percipiatur, patet ex dictis. Atque etiam in fistulis experimento comprobatur: quae si validiori flatu inspirentur quam solent, statim vna octava acutiorem edent sonum. Neque ratio est, quare immediate ad octavam deveniat potius quam ad quintam vel alias, nisi quia octava omnium prima est, & quae omnium minime differt ab vnisono.Vnde praeterea sequi existimo, nullum sonum audiri, quin huius octava acutior auribus quodammodo videatur resonare. Vnde factum est etiam in testudine, vt crassioribus nervis, qui graviores edunt sonos, alij minores adiungerentur, vna octava acutiores, qui semper una tanguntur, & efficiunt vt graviores distinctius audiantur. Ex quibus patet nullum sonum, qui cum vno octavae termino consonabit, posse cum alio eiusdem octavae dissonare.

Alterum est in octava notandum: nempe illa consonantiarum omnium maximam esse, id est, omnes alias in illa contineri, vel ex illa componi & alijs quae in ea continentur. Quod demonstrari potest ex eo, quod consonantiae omnes constent partibus aequalibus; vnde sit vt, si illarum termini amplius quam vna octava distent ab invicem, possim absque vlla divisione vlteriori gravioris termini vnam octavam acutiori addere, ex qua vna cum residuo illam componi apparebit. Exemplum sit A B, divisus in tres aequales partes, ex quibus A C, A B, distent vna duodecima: dico illam duodecimam componi ex octava & ejus residuo, nempe quinta. Componitur enim ex A C, A D, quod est octava, & ex A D, A B, quod est quinta; & ita accidit in caeteris.

Vnde sit vt octava non ita multiplicet numeros proportionum, si alias componat, quam caeterae omnes; ideoque sola sit, quae possit geminari. Si enim illa geminetur, 4 tantum efficit; vel 8, si iterum geminetur. Si autem, v. g., quinta, quae post illam prima est, geminetur, 9 efficiet; nam a 4 ad 6 est quinta; item a 6 ad 9, qui numerus longe major est quam 4, & excedit seriem primorum sex numerorum, in quibus omnes supra consonantias inclusimus.

Ex quibus sequitur cuiuscunque generis consonantiarum tres esse species: nempe vna est simplex, alia composita a simplici & octava, tertia composita a simplici & duabus octavis. Nec vlterius alia species additur, quae componatur a tribus octavis & alia consonantia simplici, quia hi sunt limites, nec vltra tres octavas sit progressio: quia scilicet tunc nimis multiplicarentur numeri proportionum. Vnde deducitur omnium omnino consonantiarum catalogus generalis, quem in sequenti Tabula expressi:

Hic sextam minorem addidimus, quam tamen nondum inveneramus in superioribus. Sed illa potest educi ex dictis de octava: a qua si ditonus abscindatur, residuum erit sexta minor. Sed mox clarius.

Nunc vero, cum iam iam dixerim omnes consonantias in octava contineri, videndum est quomodo id fiat, & quomodo ex illius divisione procedant, vt illarum natura distinctius agnoscatur.

Primum autem, ex praenotatis, certum est id fieri debere per divisionem Arithmeticam, siue in aequalia. Quid autem sit quod dividi debeat, patet in nervo A B, quod distat ab A C, parte C B; sonus autem A B distat a sono A C vna octava; ergo spatium octavae erit pars soni C B. Illa est igitur quae dividi debet in duo aequalia, vt tota octava dividatur: quod factum est in D. Ex qua divisione vt sciamus quae consonantia proprie & per se generetur, considerandum est A B, qui gravior est terminus, dividi in D: non in ordine ad se ipsum, tunc enim divideretur in C, vt ante factum est; neque enim jam dividitur vnisonus, sed octava, quae duobus constat terminis, ideoque, dum gravior terminus dividitur, id fit in ordine ad alium acutiorem, non ad se ipsum. Vnde fit vt consonantia, quae ex illa divisione proprie generatur, sit inter terminos A C, A D, quae est quinta, non inter A D, A B, quae quarta est: quia pars D B est tantum residuum, & per accidens consonantiam generat, ex eo quod ille sonus, qui cum vno octavae termino consonantiam efficit, etiam cum alio debeat consonare.

Rursum vero, divisio spatio C B in D, potero eadem ratione dividere C D in E: vnde directe generabitur ditonus, & per accidens reliquae omnes consonantiae. Nec vlterius idcirco C E opus est dividere. Quod si tamen fieret, v. g., in F, inde oriretur tonus maior, & per accidens minor, & femitonia, de quibus postea. In voce enim successiva admittuntur, non in consonantijs.

Neque quis putet immaginarium illud quod dicimus, proprie tantum ex divisione octavae quintam generari & ditonum, caeteras per accidens. Id enim etiam experientia compertum habeo, in nervis testudinis vel alterius cuiuslibet instrumenti: quorum vnus si pulsetur, vis ipsius soni concutiet omnes nervos qui aliquo genere quintae vel ditoni erunt acutiores; in ijs autem qui quarta vel alia consonantia distabunt, id non fiet. Quae certe vis consonantiarum non nisi ex illarum perfectione potest oriri vel imperfectione, quae scilicet primae per se consonantiae sint, aliae autem per accidens, quia ex alijs necessario fluunt.

Videndum autem est, vtrum id verum sit quod supra dixi, omnes consonantias simplices in octava contineri. Quod optime fiet, si C B mediam partem soni A B, quae octavam continet, volvam in circulum, ita vt punctum B cum puncto C iungatur; deinde ille circulus dividatur in D & E, vt divisum est C B. Ratio autem quare ita omnes consonantiae debent inveniri, est quia nihil consonat cum vno octavae termino, quin etiam cum alio consonet, vt supra probavimus. Vnde fit vt, si in sequenti figura vna pars circuli consonantiam efficiat, residuum etiam debeat aliquam consonantiam continere.

Ex hac figura apparet, quam recte octava diapasson appelletur: quia scilicet omnia consonantiarum aliarum intervalla in se complectitur. Hic autem consonantias simplices tantum adhibuimus, vbi si compositas etiam velimus invenire, oportet duntaxat cuilibet ex superioribus intervallis integrum vnum circulum vel duos integros adiungere; vbi apparebit octavam omnes consonantias componere.

Ex iam dictis elicimus omnes consonantias ad tria genera posse referri: vel enim oriuntur ex prima divisione vnisoni, illae quae octavae appellantur, & hoc est primum genus; vel 2°, oriuntur ex ipsius octavae divisione in aequalia, quae sunt quintae & quartae, quas idcirco consonantias secundae divisionis vocare possumus; vel denique, ex ipsius quintae divisione, quae consonantiae sunt tertiae & ultimae divisionis.

Rursum divisimus in illas quae per se ex illis divisionibus oriuntur, & in illas quae per accidens; tresque duntaxat per se consonantias esse diximus: quod etiam poetst confirmari ex prima figura, in qua consonantias ex numeris ipsis elicuimus. In illa enim advertendum est, tres esse duntaxat numeros sonoros, 2, 3 & 5; numerus enim 4 & numerus 6 ex illis componuntur, atque ideo tantum per accidens numeri sunt sonori: vt ibi etiam patet, vbi in recto ordine & in recta linea non generant novas consonantias, sed duntaxat illas quae ex prioribus componuntur. V. g., 4 generat decimam quintam, 6 autem decimam nonam; per accidens autem & in linea transversa, 4 generat quartam, & 6 tertiam minorem. Vbi obiter notandum in numero 4 quartam immediate ab octava generari, & esse veluti quoddam monstrum octavae deficiens & imperfectum.

Da quanto s’è detto è chiaro che l’ottava è di tutte le consonanze la prima ad essere facilmente percepita dopo l’unisono ⁽¹⁾. Questo è dimostrato anche dall’esperimento con le canne: se vengono insufflate più fortemente del solito, subito danno un suono più acuto d’una ottava. La ragione per cui il suono passa immediatamente all’ottava invece che a una quinta o a altri intervalli, è che l’ottava è la prima di tutte le consonanze e non differisce molto dall’unisono. Ritengo inoltre di conseguenza che non si oda suono alcuno che in qualche modo non sembri far risuonare all’orecchio la sua ottava superiore. Anche negli strumenti a corda avviene che siano affiancate alle più grosse, che rendono suoni più gravi, corde minori più acute d’una ottava, che si pizzicano sempre contemporaneamente, e fanno sì che i suoni più gravi siano percepiti più distintamente ⁽²⁾. È evidente dalle cose dette che nessun suono, che sia in consonanza con uno degli estremi dell’ottava, possa essere dissonante con l’altro estremo della stessa ottava.

La seconda cosa da notare è che l’ottava è la più grande di tutte le consonanze, ossia le contiene tutte, ovvero esse si formano dall’unione dell’ottava con quelle che essa contiene. Lo si può dimostrare in base al fatto che tutte le consonanze sono costituite di parti uguali: per cui se i loro estremi distano più dell’intervallo d’ottava, posso aggiungere un’ottava all’estremo più acuto senza dividere ulteriormente l’estremo più grave, onde essa risulterà composta da questa sola ottava e il residuo. L’esempio è AB diviso in 3 parti uguali:

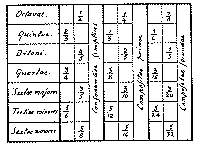
di cui AC, AB distano d’una 12esima: dico che questa 12esima è composta dall’ottava più un suo resto, ossia la quinta. Infatti è composta da AC, AD che è l’ottava, e da AD, AB che è la quinta, e così avviene per le altre.

[...]

Dalle cose dette segue che tre sono le specie di ciascun genere di consonanza: semplice, composta dalla semplice e da un’ottava, infine composta dalla semplice e da due ottave. Non se ne possono aggiungere altre composte da tre ottave e una semplice, perché i confini sono questi, né si dà progressione oltre le tre ottave, altrimenti i termini delle proporzioni si moltiplicherebbero. Se ne può dedurre il seguente catalogo generale di tutte le consonanze, riprodotto nella tavola seguente:

Abbiamo aggiunto qui la sesta minore, che non avevamo incontrato nelle divisioni precedenti. Ma questa può essere dedotta dalle cose dette a proposito dell’ottava, da cui tolto il ditono rimarrà la sesta minore, come tra breve sarà più chiaro.

Ora infatti, poiché ho appena detto che tutte le consonanze sono contenute nell’ottava, dobbiamo vedere come questo avvenga, e come derivino dalla divisione dell’ottava, affinché la loro natura sia conosciuta più chiaramente.

Per prima cosa, dalle premesse è chiaro che la divisione deve essere aritmetica, ossia in parti uguali. Ma qual sia ciò che si debba dividere si vede nella corda AB:

AB dista da AC della parte CB; quindi l’intervallo tra AB e AC è un’ottava. Lo spazio dell’ottava sarà dunque il suono CB. Questa è perciò l’ottava che deve essere divisa in due parti uguali, affinché tutta l’ottava sia divisa, ciò che si è fatto in D. Per sapere quale consonanza sia generata direttamente (proprie et per se) da questa divisione, dobbiamo considerare il termine più grave AB diviso in D: non in relazione a se stesso, ché in tal caso si sarebbe diviso in C, come s’è fatto prima; non si divide infatti l’unisono ma l’ottava, che consiste di due termini, per cui quando si divide il termine più grave, questa divisione avviene in ordine al termine più acuto, non a se stesso. Ne segue che la consonanza che si genera direttamente (proprie) da questa divisione è tra gli estremi AC, AD, che è una quinta, non tra AD, AB, che è una quarta; perché la parte DB è solo il resto e genera la consonanza indirettamente (per accidens), in quanto il suono che produce consonanza con uno degli estremi dell’ottava deve essere in consonanza anche con l’altro.

Di nuovo, diviso lo spazio CB in D, potrò per la stessa ragione dividere CD in E. Da questa divisione si genera direttamente la terza maggiore, e per accidente tutte le rimanenti consonanze. Non è necessario dividere ulteriormente CE. Se tuttavia lo si suddivide, come in F, ne nascerebbe il tono maggiore e ‘per accidens’ il minore, quindi i semotoni, di cui parlerò oltre (Cap. X).

Qualcuno non pensi che quanto s’è detto sia immaginario, vale a dire che dalla divisione dell’ottava si generano direttamente solo la quinta e la terza maggiore, le rimanenti ‘per accidens’. Per esperienzia so bene che nelle corde del liuto o di qualche altro strumento simile, se una di esse viene pizzicata, la forza dello stesso suono colpirà le corde che sono più acute di qualche genere di quinta o di terza maggiore; e questo non si verifica nelle corde a intervallo di quarta o d’altra consonanza. La qual forza delle consonanze non può nascere se non dalla loro perfezione o imperfezione, appunto perché le prime sono consonanze per sè, le altre invevce per accidente, in quanto derivano necessariamente dalle altre

[...]

Abbiamo poi diviso le consonanze in consonanze per sè e per accidente, e s’è detto che tre soltanto sono le consonanze per sè: ciò è confermato anche dalla prima figura, nella quale abbiamo trovato le consonanze dagli stessi numeri. In quella figura bisogna notare che tre sono appunto i numeri sonori, 2, 3 e 5; infatti il 4 e il 6 sono dei composti, e perciò sono numeri sonori solo per accidente: infatti nella figura è evidente che sulla linea verticale il 4 e il 6 non generano nuove consonanze ma solo quelle composte delle precedenti: Ad esempio, 4 genera la 15esima, il 6 la 19esima; invece, per accidens e sull’orizzontale, il 4 genera la quarta e il 6 la terza minore. Dove di passaggio bisogna notare nel numero 4 che la quarta è generata immediatamente dall’ottava, ed è quasi il prodotto difettoso e imperfetto dell’ottava