Advertendum est, primo, vnisonum non esse consonantiam, quia in illo nulla est differentia sonorum in acuto & gravi; sed illum se habere ad consonantias, vt vnitas ad numeros.

Secundo, ex duobus terminis, qui in consonantia requiruntur, illum qui gravior est, longe esse potentiorem, atque alium quodammodo in se continere. Vt patet in nervis testudinis, ex quibus dum aliquis pulsatur, qui illo octava vel qiunta acutiores sunt, sponte tremunt & resonant; graviores autem non ita, saltem apparenter. Cuius ratio sic demonstratur: sonus se habet ad sonum, vt nervus ad nervum; atqui in quolibet nervo omnes illo minores continentur, non autem longiores; ergo etiam in quolibet sono omnes acutiores continentur, non autem contra graviores in acuto. Vnde patet acutiorem terminum esse inveniendum per divisionem gravioris; quam divisionem debere esse arithmeticam, hoc est in aequalia, sequitur ex praenotatis.

Sit igitur A B gravior terminus; in quo si velim acutiorem terminum primae consonantiarum omnium invenire, illum dividam per primum numerorum omnium, nempe per binarium, vt factum est in C: & tunc A C, A B, prima consonantiarum omnium distant ab invicem, quae octava & diapasson appellatur. Quod si rursum alias consonantias habere velim, quae immediate secuuntur primam, dividam A B in tres partes aequales: tuncque non habebo duntaxat vnum acutum terminum, sed duos, nempe A D & A E; ex quibus nascentur duae consonantiae huiusdem generis, nempe duodecima & quinta. Rursus possum dividere lineam A B in quatuor partes, vel in quinque, vel in sex; nec vlterius sit divisio, quia scilicet aurium imbecilitas fine labore majores sonorum differentias non posset distinguere.

Vbi notandum est, ex prima divisione oriri tantum vnam consonantiam; ex secunda, duas; ex tertia, tres, &c., vt sequens Tabula demonstrat:

Hic nondum omnes consonantiae sunt; sed vt reliquas inveniamus, agendum est prius

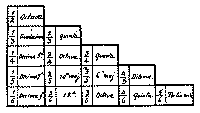
In primo luogo va detto che l’unisono non è consonanza, perché nell’unisono non c’è differenza alcuna nell’acuto e nel grave, ma sta alle consonanze come l’unità ai numeri ⁽¹⁾

Secondo, di due estremi che si vogliono in consonanza, quello più grave è di gran lunga più potente, e in qualche modo contiene in sé l’altro. Come si vede nelle corde della lira, delle quali quando una è pizzicata quelle più acute all’ottava o alla quinta tremano spontaneamente e risuonano, mentre le più gravi non fanno così. La ragione si dimostra così: il suono sta al suono come la corda sta alla corda; ora in ogni corda sono contenute le minori, non le più lunghe; perciò anche in un suono sono contenuti i suoni più acuti, non al contrario i più gravi sono contenuti nell’acuto. Ne viene che il termine più acuto deve essere trovato attraverso la divisione del più grave, la qual divisione deve essere aritmetica, ossia in parti uguali, come segue dalle premesse. ⁽²⁾

Sia pertanto AB il termine più grave; se voglio trovare il termine più acuto, dividerò AB per il primo di tutti i numeri, il binario ⁽³⁾, come è stato fatto in C:

Allora AC, AB distano tra loro della prima di tutte le consonanze, ottava o diapason. Se poi di nuovo volessi ottenere le altre consonanze che seguono immediatamente la prima, dividerò AB in tre parti uguali: allora non avrò un solo termine acuto, ma due, ossia AD e AE, dai quali nasceranno due consonanze dello stesso genere, la dodicesima e la quinta. Di nuovo posso dividere la linea AB in quattro parti, o in cinque, o ancora in sei, senza procedere nella divisione, perché il limite dell’udito non saprebbe distinguere senza difficoltà troppo grandi differenze di suoni.

Qui si deve notare che dalla prima divisione si è formata una sola consonanza, dalla seconda due, dalla terza tre, e così via, come mostra la tabella:

Nella figura non ci sono ancora tutte le consonanze; per trovarle cominciamo a considerare l’ottava.